ECUACIONES DE LA HIPÉRBOLA.!
Ecuaciones en coordenadas cartesiana Ecuación de una hipérbola con centro en el origen de coordenadas
y ecuación de la hipérbola en su forma canonica.
Ecuación de una hipérbola con centro en el punto 
Ejemplos:
a)
b)
Si el semieje transverso a se encuentra en el eje x, y el semieje conjugado b, en el eje y, entonces la hipérbola es horizontal; si es al revés, es vertical. La excentricidad de una hipérbola siempre es mayor que uno.
Ecuación de la hipérbola en su forma compleja
Una hipérbola en el plano complejo es el lugar geométrico formado por un conjunto de puntos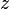 
, en el plano 
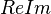; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias 
, a dos puntos fijos llamados focos
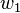y 
, es una constante positiva igual al doble de la distancia (o sea 
) que existe entre su centro y cualesquiera de sus vértices del eje focal.
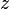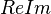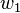, en el plano ; tales que, cualesquiera de ellos satisface la condición geométrica de que el valor absoluto de la diferencia de sus distacias , a dos puntos fijos llamados focos y , es una constante positiva igual al doble de la distancia (o sea ) que existe entre su centro y cualesquiera de sus vértices del eje focal.
La ecuación queda: 
Evidentemente esta operación se lleva a cabo en el conjunto de los números complejos.
- Pero como aplicamos la Hiperbola en nuestro dia a dia bueno las tenemos en la nariz de nuestro perro, el enfoque de la luz de una lampara hace una hiperbola tambien en muchas estructuras de edificios,etc.
No hay comentarios:
Publicar un comentario